DAG = Tree?
Refer this link for all DSA articles
DAGs
source — https://youtu.be/eQA-m22wjTQ
DAGS are directed graphs with no cycles. These graphs play an important role in representing structures with dependencies. Several efficient algorithms exist to operate on DAGS .
These graphs play an important role in representing structures with dependencies.
Cool fact: All out-trees are DAGS but not all DAGS are out-trees.

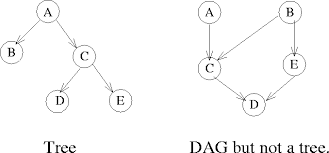
- From this view, both trees and DAGs are connected, directed, rooted, and have no cycles so this means that starting from any node and going up the parents you will eventually work your way up to the top (root).
- However, since DAG nodes have multiple parents, there will be multiple paths on the way up (that eventually merge).
- So Trees are DAGs with the restriction that a child can only have one parent.
- Another way to see it is Tree is like single class inheritance, and DAG is like multiple class inheritance.
- If you were to approach this from a purely mathematical view,
→ the problem with relating these two is that those trees are defined in terms of undirected edges,
→ but DAGs are defined in terms of directed edges,
→ so they are hard to compare without getting more detailed. - If you took a DAG with double paths and changed edges from directed to undirected (to make it like a tree), the tree would now have cycles, i.e., it is no longer a tree.
- A tree is a DAG whose undirected version is still acyclic.